60년 수학 난제 ‘소파 문제’ 푼 한국인 연구, 10대 수학 혁신 사례로

60년 가까이 수학 난제로 꼽힌 ‘소파 움직이기 문제’를 해결한 백진언(31) 박사 연구가 지난해 10대 수학 혁신 사례로 선정됐다.

4일 수학계에 따르면 미국 과학 전문지 ‘사이언티픽 아메리칸’은 지난해 10대 수학 혁신 사례로 고등과학원 허준이수학난제연구소의 백 박사(허준이펠로우) 연구를 선정했다.

백진언 박사. 고등과학원 ‘호라이즌’ 홈페이지 캡처 소파 움직이기 문제는 폭이 1인 직각 형태 복도를 통과할 수 있는 최대 면적의 도형 ‘이상적인 소파’를 찾는 문제다. 1966년 캐나다 수학자 레오 모저가 처음 제시했고, 이해하기 쉬워 미국 수학 교과서에 실리기도 했다. 수학자들은 유선 전화기 모양의 소파가 이상적이라고 제시했지만 이론으로 이를 검증하지는 못했다.

앞서 1992년 수학자 조셉 거버 럿거스대 교수가 소파가 벽에 닿는 순서를 고려해 최적화한 18개 곡선으로 만든 2.2195 면적의 ‘거버의 소파’를 제시했지만, 최적의 답인지는 증명되지 않았다.

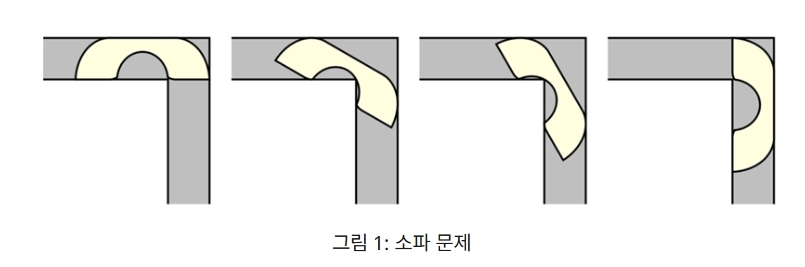소파 움직이기 문제. 백 박사는 7년간 이 문제에 도전한 끝에 2024년 11월 연세대 박사후연구원 시절 ‘거버의 소파보다 더 넓은 소파는 없다’는 증명이 담긴 논문을 논문 사전공개 사이트 ‘아카이브’에 발표했다.

문제 해결에 대한 직관은 연구를 시작하고 3년 만에 떠올랐지만 이를 수학적으로 증명하고 논문으로 정리하는 데 시간이 걸렸다고 한다. 기존 연구가 컴퓨터를 이용해 소파 최대 크기를 좁히는 데 주력했는데, 백 박사는 논리적 추론을 통해 이상적인 소파를 입증했다.

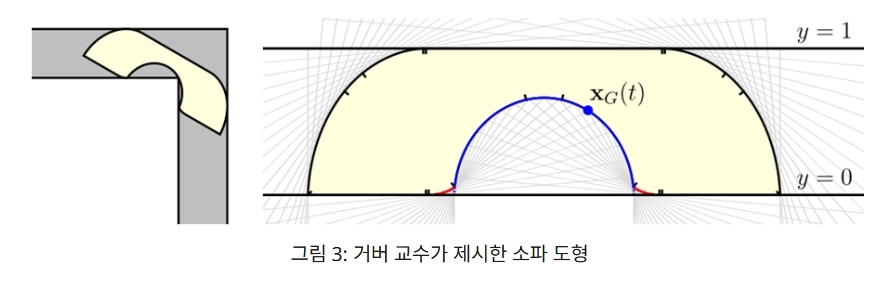조셉 거버 교수가 제시한 소파 도형. 이번 연구는 수학계 최고 학술지 ‘수학 연보’에 투고돼 검증을 기다리고 있다. 수학계에선 백 박사의 증명이 맞을 가능성이 높다고 본다.

백 박사는 지난해 8월 만39세 이하의 젊은 수학자를 최대 10년간 지원하는 ‘허준이펠로우’로 선정돼 조합적 기하학에 있는 최적화 문제와 난제 풀이에 도전하고 있는 것으로 알려졌다. 백 박사는 고등과학원이 발간하는 과학전문 웹진 ‘호라이즌’에 게재된 인터뷰에서 “초등학교 3, 4학년 때 수학을 직업으로 할 수 있다는 걸 알게 된 이후로 계속 꿈이 수학자였던 것 같다”며 “다른 직업을 하더라도 수학이라는 아름다움은 놓지 못했을 것 같다”고 했다.

이정한 기자 han@segye.com